(a, d) Spatial distribution of eigen wavefunctions along the z ![]()
![]()
Ω=0.5Er ![]()
![]()
Γz=5Er ![]()
![]()
z∈[−30,30] ![]()
![]()
480 ![]()
![]()
ρ∈[0,4] ![]()
![]()
8 ![]()
![]()
800 ![]()
![]()
Re(E) ![]()
![]()
˜ψ1(z)=2π∫ρdρψ1(ρ,z) ![]()
![]()
t=0.6 ![]()
![]()
vm≈16.04 ![]()
![]()
vm≈13.33 ![]()
![]()
ω=ω0=100 ![]()
![]()
ω=2ω0=200 ![]()
![]()
10 ![]()
![]()
6 ![]()
![]()
Figures of the Article
-
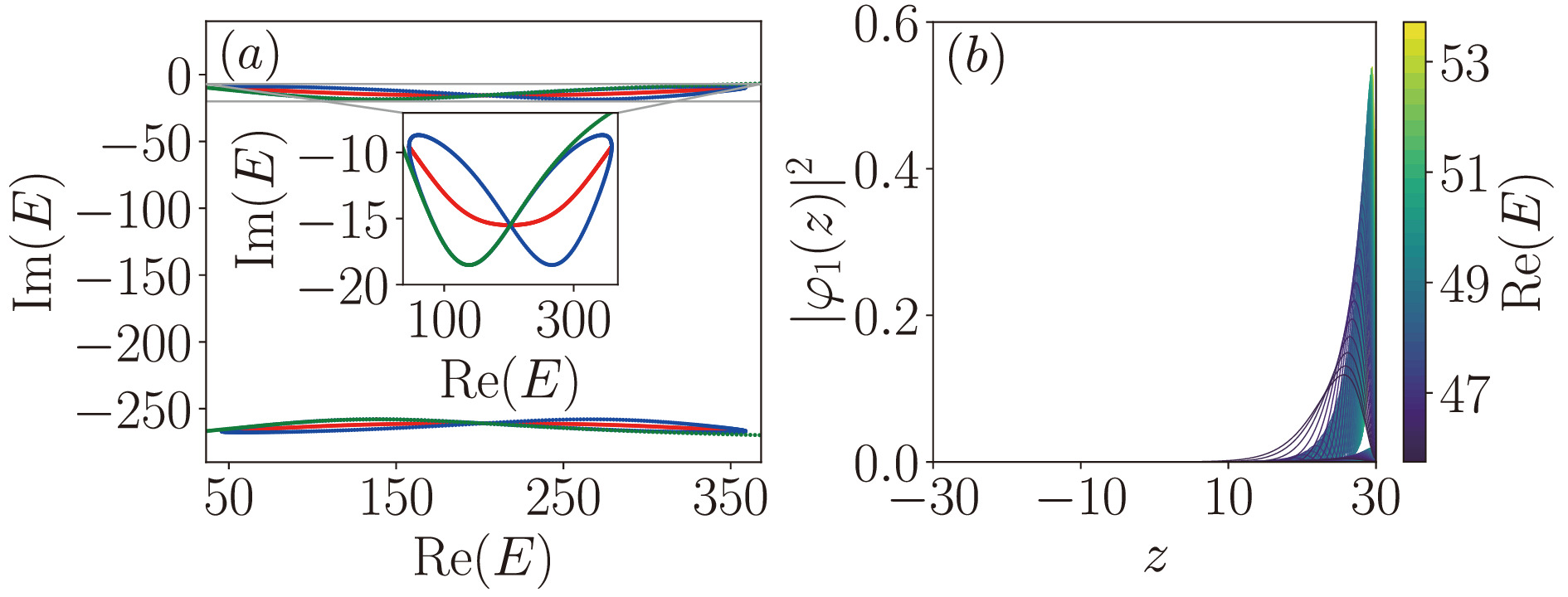
![]() (a) Single-particle eigenspectra of Hamiltonian (1) on the complex plane. Green: eigenspectrum of in the momentum space (an infinite system under PBC). Blue: eigenspectrum of a finite system with
(a) Single-particle eigenspectra of Hamiltonian (1) on the complex plane. Green: eigenspectrum of in the momentum space (an infinite system under PBC). Blue: eigenspectrum of a finite system with z∈[−30,30] . Red: eigenspectrum under OBC. Inset: enlarged eigenspectra. We fixΩ=0.5Er andΓz=2Er . For calculations of finite systems, the spatial coordinates alongz are discretized into480 segments. (b) Spatial distribution of the100 eigenstates with the smallest real components (indicated by the color bar). -
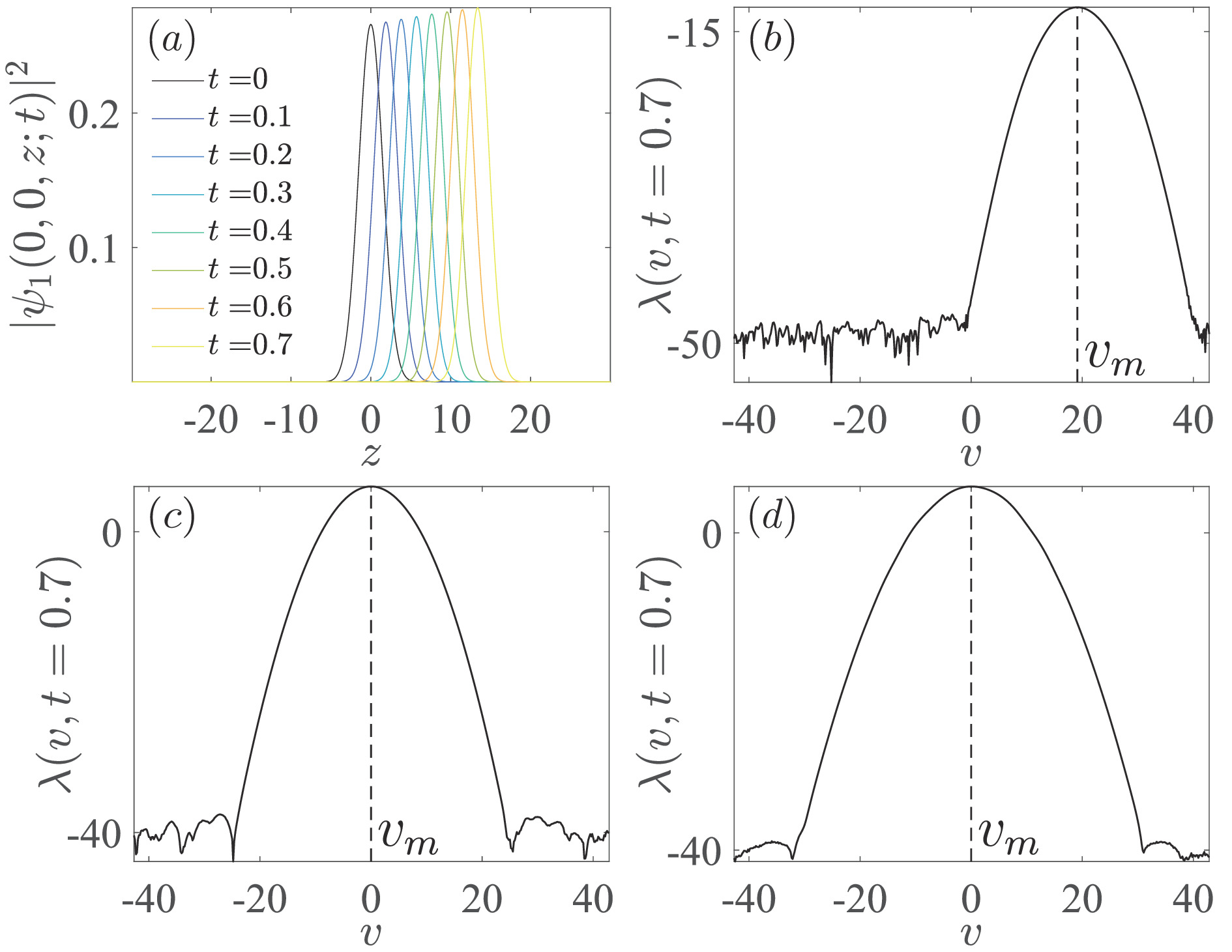
![]() (a) Propagation of the condensate wavefunction in the bulk, with
(a) Propagation of the condensate wavefunction in the bulk, with Ω=0.5Er andΓz=2Er . (b) Growth rate as a function of the shift velocity under the parameters of (a). (c) Growth rate withΩ=0 andΓz=2Er , evaluated att=0.7 . (d) Growth rate withΩ=0.5Er andΓz=0 , valuated att=0.7 . The unit of time is1/ω0=10 ms. -
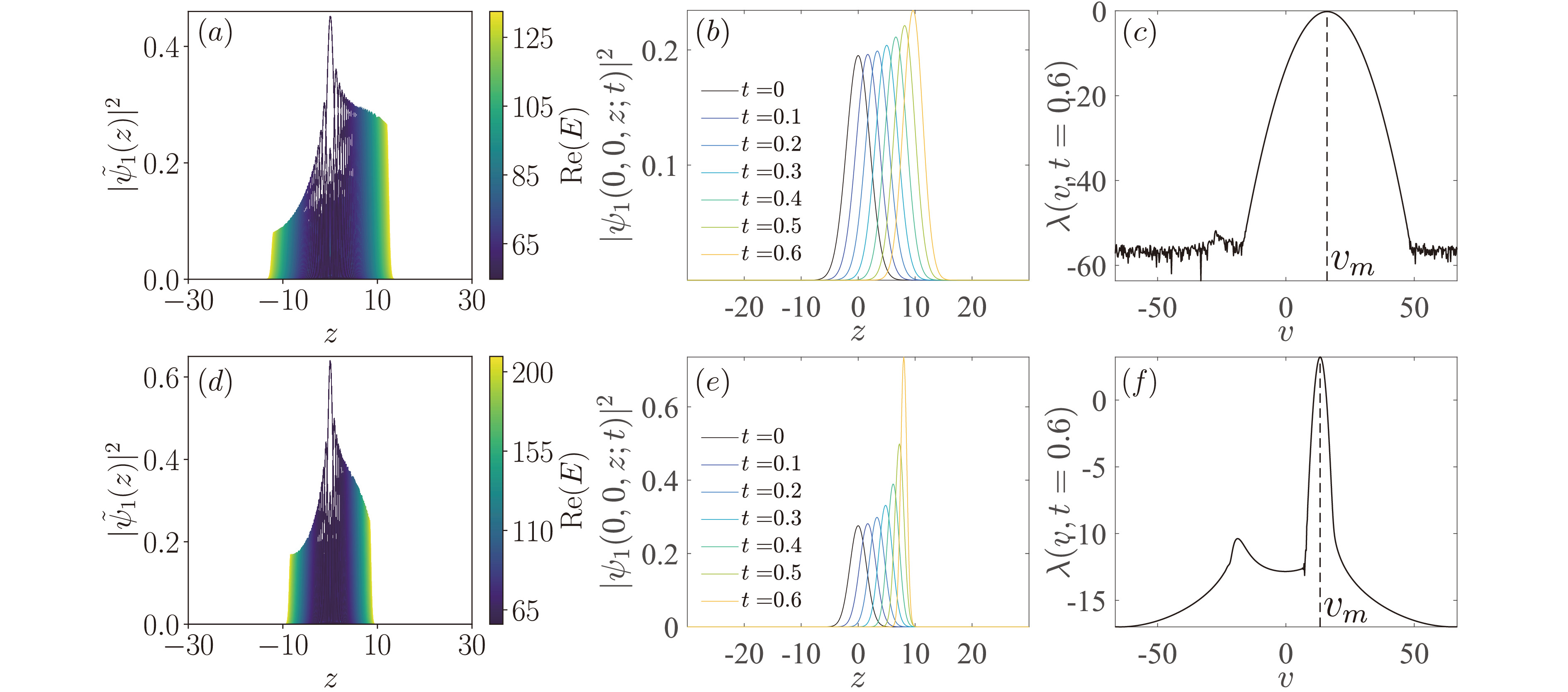
![]() (a, d) Spatial distribution of eigen wavefunctions along the
(a, d) Spatial distribution of eigen wavefunctions along the z direction in an isotropic harmonic trap, withΩ=0.5Er andΓz=5Er . For the numerical calculations here, we take a cylindrical coordinate, discretizingz∈[−30,30] into480 segments, and the radial coordinateρ∈[0,4] into8 segments. We plot the radial-integrated spatial distribution of the800 eigenstates with the smallest real components, colored according toRe(E) (see color bar). Specifically,˜ψ1(z)=2π∫ρdρψ1(ρ,z) . (b, e) Propagation of the condensate wavefunction in the bulk. (c, f) Growth rate as a function of the shift velocity att=0.6 . The peak shift velocityvm≈16.04 in (c) andvm≈13.33 in (f). The trapping potential isω=ω0=100 Hz in (a, b, c), andω=2ω0=200 Hz in (d, e, f). The unit of time is10 ms, so the longest evolution time in (b, e) is6 ms. -
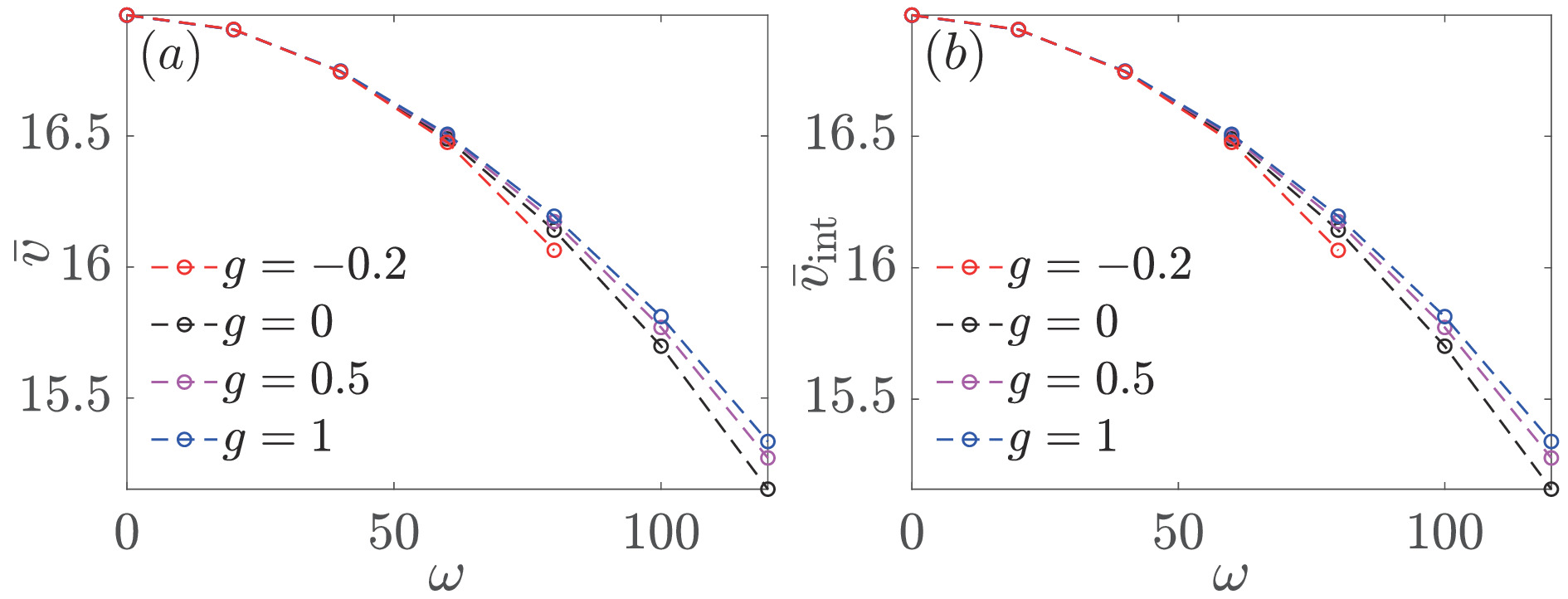
![]() Effect of condensate interaction on the non-Hermitian skin effect in a trapped gas, evaluated at
Effect of condensate interaction on the non-Hermitian skin effect in a trapped gas, evaluated at t=0.7 (∼7 ms). See main text for the definition of the average propagation speedˉv in (a), and the integrated propagation speedˉvint in (b). Other parameters are the same as those in Fig. 3.
Related articles
-
2024, 54(6): 0605. DOI: 10.52396/JUSTC-2024-0046
-
2024, 54(6): 0601. DOI: 10.52396/JUSTC-2024-0025
-
2023, 53(10): 1001. DOI: 10.52396/JUSTC-2023-0098
-
2022, 52(4): 1-1-1-7. DOI: 10.52396/JUSTC-2021-0239
-
2021, 51(11): 822-830. DOI: 10.52396/JUST-2021-0126
-
2020, 50(8): 1138. DOI: 10.3969/j.issn.0253-2778.2020.08.014
-
2019, 49(12): 957-964. DOI: 10.3969/j.issn.0253-2778.2019.12.002
-
2017, 47(2): 87-98. DOI: 10.3969/j.issn.0253-2778.2017.02.001
-
2013, 43(11): 861-869. DOI: 10.3969/j.issn.0253-2778.2013.11.001



 Download:
Download: