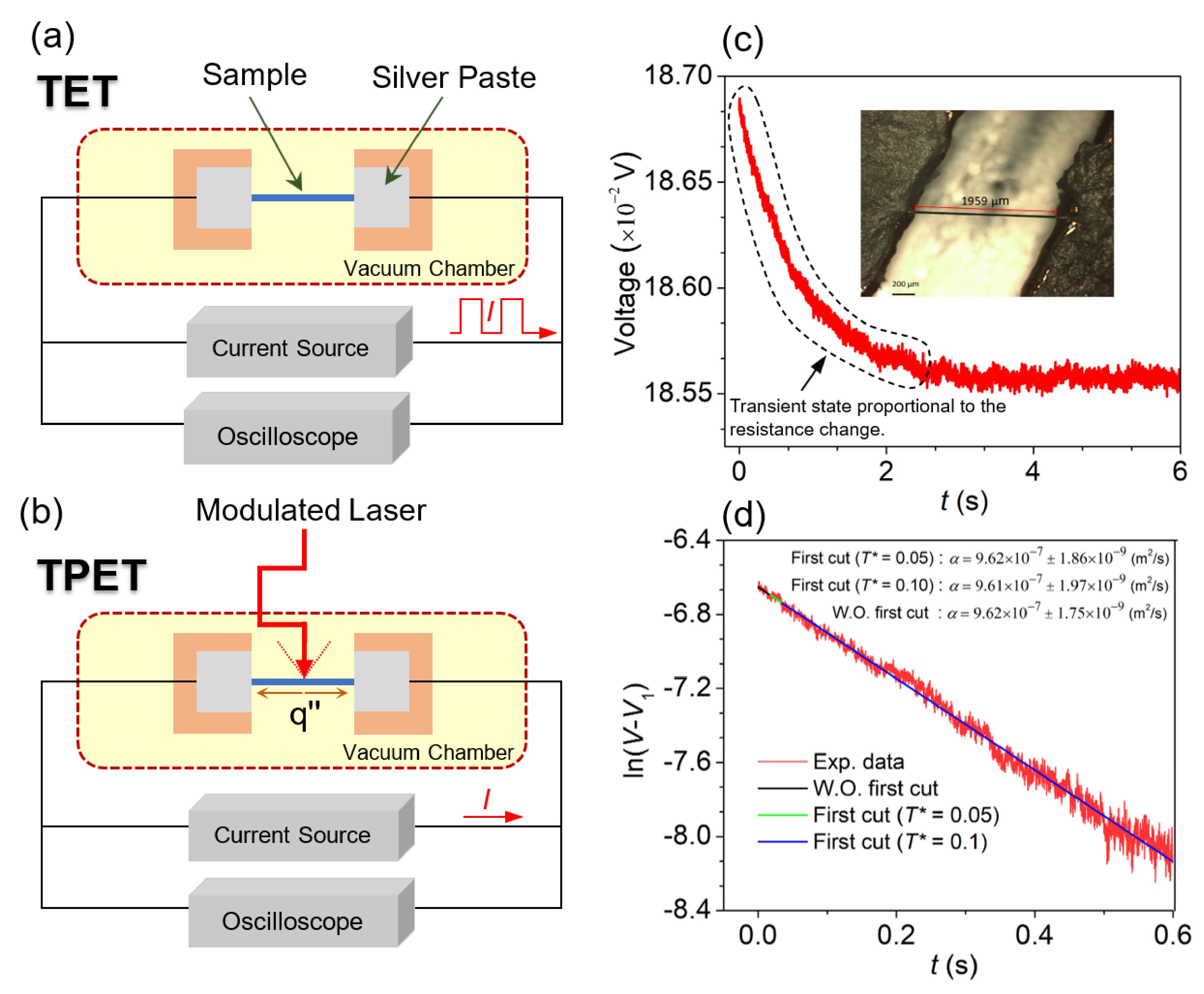
ISSN 0253-2778
CN 34-1054/N
CO2+HFC binary mixtures have good performance and environmental friendliness and are considered good alternative working fluids in cooling and power cycle systems. The vapor-liquid phase equilibrium properties are key to the calculation of the enthalpy and entropy of mixtures, which is critical for the analysis of cooling and power cycle systems. To accurately predict the vapor-liquid equilibrium of CO2 and HFC (R23, R32, R41, R125, R134a, R143a, R152a, R161, and R227ea) binary mixtures, a group contribution model based on the excess free energy (GE) mixing rules (PR+MHV1+UNIFAC and PR+LCVM+UNIFAC) is established in this paper. The interaction parameters between groups such as -CO2, -Alkane, -CHF, and -CHF3 are obtained by the vapor-liquid phase equilibrium experiment of CO2 and HFC refrigerants, and these group parameters are critical for predicting their vapor-liquid phase equilibrium properties (the pressures and vapor phase molar fractions). The AARDp value calculated by the PR+LCVM+UNIFAC model is 5.53%, the value of AADy1 is 0.0132, and the AARDp and AADy1 values of the PR+MHV1+UNIFAC model are 7.40% and 0.0229, respectively. However, for the CO2+R32 system, the PR+MHV+UNIFAC prediction model can reproduce the experimental data with lower deviations, and the values of AARDp and AADy1 are 1.53% and 0.0045, respectively. In summary, for CO2+HFC binary mixtures, the PR+LCVM+UNIFAC group contribution model can reproduce the experimental data with lower deviations, but for individual CO2 binary mixtures (such as CO2+R32), the PR+MHV1+UNIFAC model also has unique advantages. According to the prediction results of the group contribution model, the PR+LCVM+UNIFAC model has significantly improved the calculation progress compared with the PR+MHV1+UNIFAC model used in the previous system.
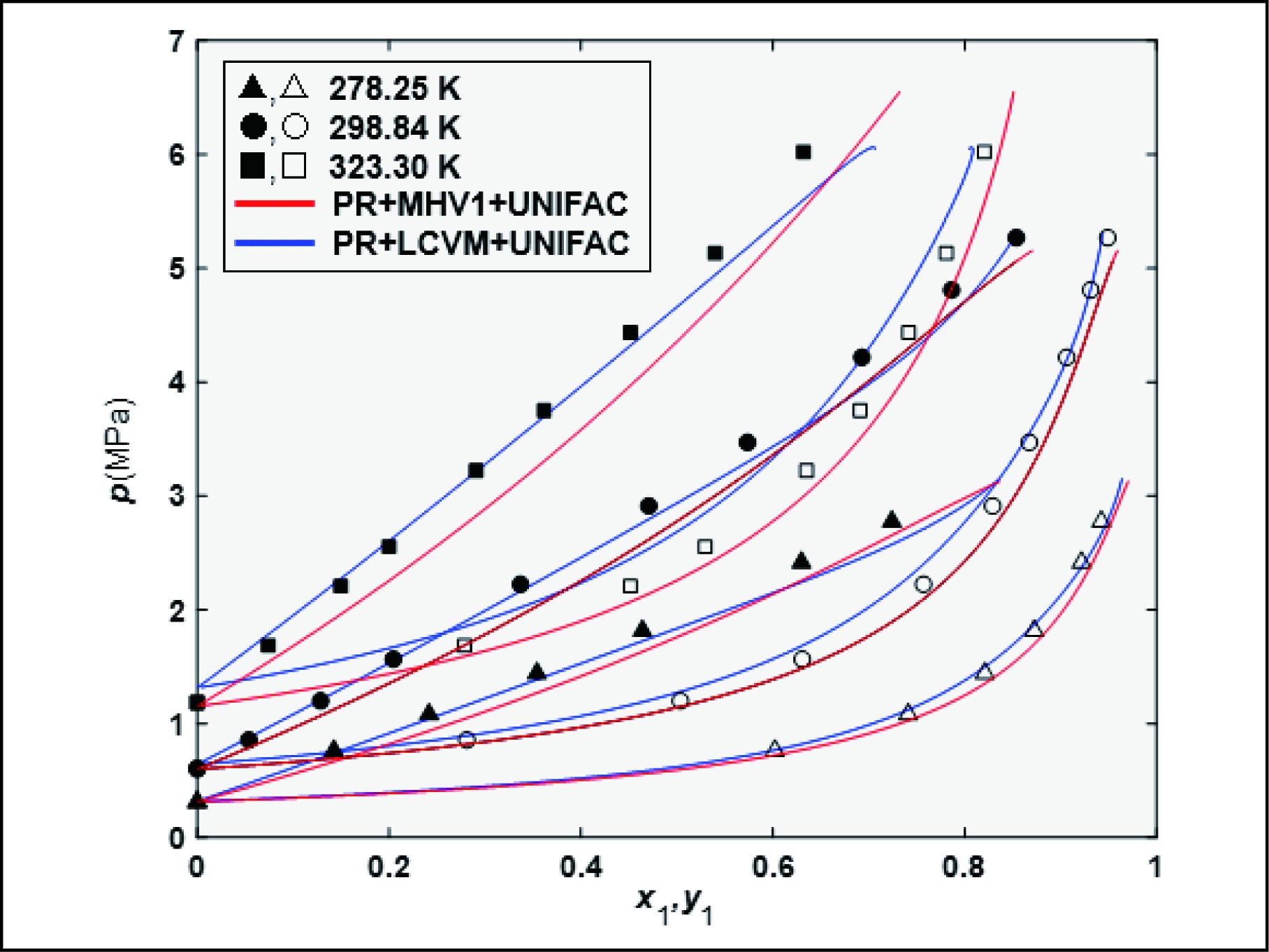
Prediction of the vapor-liquid phase equilibrium for CO2+R152a at three temperatures.
Figure 2. Prediction of the vapor-liquid phase equilibrium properties for CO2+R32 at three temperatures. Experimental data[35]: T=283.12 K (●,○); T=303.13 K (■,□). Solid red line represents the PR+MHV1+UNIFAC model; solid blue line represents the PR+LCVM+UNIFAC model.
Figure 4. Prediction of the vapor-liquid phase equilibrium properties for CO2+R152a at three temperatures. Experimental data[39]: T=278.25 K (▲,△); T=298.84 K (●,○); T=3323.30 K (■,□). Solid red line represents the PR+MHV1+UNIFAC model; solid blue line represents the PR+LCVM+UNIFAC model.
Figure 3. Prediction of the vapor-liquid phase equilibrium properties for CO2+R143a at three temperatures. Experimental data[38]: T=273.15 K (●,○); T=303.15 K (■,□). Solid red line represents the PR+MHV1+UNIFAC model; solid blue line represents the PR+LCVM+UNIFAC model.
| [1] |
Wang S, Fauve R, Coquelet C, et al. Vapor-liquid equilibrium and molecular simulation data for carbon dioxide (CO2) + trans-1,3,3,3-tetrafluoroprop-1-ene (R-1234ze(E)) mixture at temperatures from 283.32 to 353.02 K and pressures up to 7.6 MPa. International Journal of Refrigeration, 2019, 98: 362–371. DOI: 10.1016/j.ijrefrig.2018.10.032
|
| [2] |
Juntarachat N, Valtz A, Coquelet C, et al. Experimental measurements and correlation of vapor-liquid equilibrium and critical data for the CO2 + R1234yf and CO2 + R1234ze(E) binary mixtures. International Journal of Refrigeration, 2014, 47: 141–152. DOI: 10.1016/j.ijrefrig.2014.09.001
|
| [3] |
Bellos E, Tzivanidis C. A comparative study of CO2 refrigeration systems . Energy Conversion and Management: X, 2019, 1: 100002. DOI: 10.1016/j.ecmx.2018.100002
|
| [4] |
Lim J S, Jin J M, Yoo K P. VLE measurement for binary systems of CO2 + 1,1,1,2-tetrafluoroethane (HFC-134a) at high pressures. The Journal of Supercritical Fluids, 2008, 44: 279–283. DOI: 10.1016/j.supflu.2007.09.025
|
| [5] |
Dai B, Liu C, Liu S, et al. Life cycle techno-enviro-economic assessment of dual-temperature evaporation transcritical CO2 high-temperature heat pump systems for industrial waste heat recovery. Applied Thermal Engineering, 2023, 219: 119570. DOI: 10.1016/j.applthermaleng.2022.119570
|
| [6] |
Wu Z, Shi L, Sun R, et al. A temperature-independent prediction model predicts the vapor-liquid equilibrium of CO2-based binary mixtures. International Journal of Refrigeration, 2022, 140: 125–138. DOI: 10.1016/j.ijrefrig.2022.05.005
|
| [7] |
Peng D Y, Robinson D B. A new two-constant equation of state. Industrial & Engineering Chemistry Fundamentals, 1976, 15: 59–64. DOI: https://doi.org/10.1021/i160057a011
|
| [8] |
Kontogeorgis G M, Coutsikos P. Thirty years with EoS/GE models—What have we learned? Industrial & Engineering Chemistry Research, 2012, 51: 4119–4142. DOI: https://doi.org/10.1021/ie2015119
|
| [9] |
Kwak T Y, Mansoori G A. Van der Waals mixing rules for cubic equations of state. Applications for supercritical fluid extraction modelling. Chemical Engineering Science, 1986, 41: 1303–1309. DOI: 10.1016/0009-2509(86)87103-2
|
| [10] |
Huron M J, Vidal J. New mixing rules in simple equations of state for representing vapour-liquid equilibria of strongly non-ideal mixtures. Fluid Phase Equilibria, 1979, 3: 255–271. DOI: 10.1016/0378-3812(79)80001-1
|
| [11] |
Wong D S H, Sandler S I. A theoretically correct mixing rule for cubic equations of state. AIChE Journal, 1992, 38: 671–680. DOI: 10.1002/aic.690380505
|
| [12] |
Michelsen M L. A method for incorporating excess Gibbs energy models in equations of state. Fluid Phase Equilibria, 1990, 60: 47–58. DOI: 10.1016/0378-3812(90)85042-9
|
| [13] |
Michelsen M L. A modified Huron-Vidal mixing rule for cubic equations of state. Fluid Phase Equilibria, 1990, 60: 213–219. DOI: 10.1016/0378-3812(90)85053-D
|
| [14] |
Boukouvalas C, Spiliotis N, Coutsikos P, et al. Prediction of vapor-liquid equilibrium with the LCVM model: A linear combination of the Vidal and Michelsen mixing rules coupled with the original UNIF. Fluid Phase Equilibria, 1994, 92: 75–106. DOI: 10.1016/0378-3812(94)80043-X
|
| [15] |
Farajnezhad A, Afshar O A, Khansary M A, et al. Correlation of interaction parameters in Wilson, NRTL and UNIQUAC models using theoretical methods. Fluid Phase Equilibria, 2016, 417: 181–186. DOI: 10.1016/j.fluid.2016.02.041
|
| [16] |
Renon H, Prausnitz J M. Local compositions in thermodynamic excess functions for liquid mixtures. AIChE Journal, 1968, 14: 135–144. DOI: 10.1002/aic.690140124
|
| [17] |
Fredenslund A, Jones R L, Prausnitz J M. Group-contribution estimation of activity coefficients in nonideal liquid mixtures. AIChE Journal, 1975, 21: 1086–1099. DOI: 10.1002/aic.690210607
|
| [18] |
Lohmann J, Joh R, Gmehling J. From UNIFAC to modified UNIFAC (dortmund). Industrial & Engineering Chemistry Research, 2001, 40: 957–964. DOI: https://doi.org/10.1021/ie0005710
|
| [19] |
Lohmann J, Gmehling J. Modified UNIFAC (dortmund). reliable model for the development of thermal separation processes. Journal of Chemical Engineering of Japan, 2001, 34: 43–54. DOI: 10.1252/jcej.34.43
|
| [20] |
Wittig R, Lohmann J, Joh R, et al. Vapor–liquid equilibria and enthalpies of mixing in a temperature range from 298.15 to 413.15 K for the further development of modified UNIFAC (dortmund). Industrial & Engineering Chemistry Research, 2001, 40: 5831–5838. DOI: https://doi.org/10.1021/ie010444j
|
| [21] |
Constantinescu D, Gmehling J. Addendum to “further development of modified UNIFAC (dortmund): Revision and extension 6”. Journal of Chemical & Engineering Data, 2017, 62: 2230. DOI: https://doi.org/10.1021/acs.jced.7b00403
|
| [22] |
Fischer K, Gmehling J. Further development, status and results of the PSRK method for the prediction of vapor-liquid equilibria and gas solubilities. Fluid Phase Equilibria, 1995, 112: 1–22. DOI: 10.1016/0378-3812(95)02792-D
|
| [23] |
Li J, Fischer K, Gmehling J. Prediction of vapor-liquid equilibria for asymmetric systems at low and high pressures with the PSRK model. Fluid Phase Equilibria, 1998, 143: 71–82. DOI: 10.1016/S0378-3812(98)00206-4
|
| [24] |
Chen J, Fischer K, Gmehling J. Modification of PSRK mixing rules and results for vapor-liquid equilibria, enthalpy of mixing and activity coefficients at infinite dilution. Fluid Phase Equilibria, 2002, 200: 411–429. DOI: 10.1016/S0378-3812(02)00048-1
|
| [25] |
Horstmann S, Jabłoniec A, Krafczyk J, et al. PSRK group contribution equation of state: Comprehensive revision and extension IV, including critical constants and α-function parameters for 1000 components. Fluid Phase Equilibria, 2005, 227: 157–164. DOI: 10.1016/j.fluid.2004.11.002
|
| [26] |
Ahlers J, Gmehling J. Development of a universal group contribution equation of state III. prediction of vapor–liquid equilibria, excess enthalpies, and activity coefficients at infinite dilution with the VTPR model. Industrial & Engineering Chemistry Research, 2002, 41: 5890–5899. DOI: https://doi.org/10.1021/ie0203734
|
| [27] |
Schmid B, Schedemann A, Gmehling J. Extension of the VTPR group contribution equation of state: Group interaction parameters for additional 192 group combinations and typical results. Industrial & Engineering Chemistry Research, 2014, 53: 3393–3405. DOI: https://doi.org/10.1021/ie404118f
|
| [28] |
Schmid B, Gmehling J. Present status of the group contribution equation of state VTPR and typical applications for process development. Fluid Phase Equilibria, 2016, 425: 443–450. DOI: 10.1016/j.fluid.2016.06.042
|
| [29] |
Hou S X, Duan Y Y, Wang X D. Vapor–liquid equilibria predictions for new refrigerant mixtures based on group contribution theory. Industrial & Engineering Chemistry Research, 2007, 46: 9274–9284. DOI: https://doi.org/10.1021/ie070911i
|
| [30] |
Gao Y, Li C, Xia S, et al. Estimation and correlation of phase equilibrium of CO2–hydrocarbon systems with PRMHV2-UNIFAC and PRMHV2-NRTL models. Journal of Chemical & Engineering Data, 2020, 65: 655–663. DOI: https://doi.org/10.1021/acs.jced.9b00890
|
| [31] |
Horstmann S, Fischer K, Gmehling J, et al. Experimental determination of the critical line for (carbon dioxide + ethane) and calculation of various thermodynamic properties for (carbon dioxide + n-alkane) using the PSRK model. The Journal of Chemical Thermodynamics, 2000, 32: 451–464. DOI: 10.1006/jcht.2000.0611
|
| [32] |
Fredenslund A, Gmehling J, Michelsen M L, et al. Computerized design of multicomponent distillation columns using the UNIFAC group contribution method for calculation of activity coefficients. Industrial & Engineering Chemistry Process Design and Development, 1977, 16: 450–462. DOI: https://doi.org/10.1021/i260064a004
|
| [33] |
Radfarnia H R, Bogdanic G, Taghikhnai V, et al. The UNIQUAC-NRF segmental interaction model for vapor-liquid equilibrium calculations for polymer solutions. Polim. (Zagreb), 2005, 26: 115-120. https://hrcak.srce.hr/file/929.
|
| [34] |
Roth H, Peters-Gerth P, Lucas K. Experimental vapor-liquid equilibria in the systems R22-R23, R22-CO2, CS2-R22, R23-CO2, CS2-R23 and their correlation by equations of state . Fluid Phase Equilibria, 1992, 73: 147–166. DOI: 10.1016/0378-3812(92)85045-A
|
| [35] |
Rivollet F, Chapoy A, Coquelet C, et al. Vapor-liquid equilibrium data for the carbon dioxide (CO2) + difluoromethane (R32) system at temperatures from 283.12 to 343.25 K and pressures up to 7.46 MPa. Fluid Phase Equilibria, 2004, 218: 95–101. DOI: 10.1016/j.fluid.2003.12.002
|
| [36] |
Jeong K, Im J, Lee S, et al. (Vapour + liquid) equilibria of the {carbon dioxide + pentafluoroethane (HFC-125)} system and the {carbon dioxide + dodecafluoro-2-methylpentan-3-one (NOVECTM1230)} system. The Journal of Chemical Thermodynamics, 2007, 39: 531–535. DOI: 10.1016/j.jct.2006.09.010
|
| [37] |
Duran-Valencia C, Pointurier G, Valtz A, et al. Vapor–liquid equilibrium (VLE) data for the carbon dioxide (CO2) + 1,1,1,2-tetrafluoroethane (R134a) system at temperatures from 252.95 K to 292.95 K and pressures up to 2 MPa. Journal of Chemical & Engineering Data, 2002, 47: 59–61. DOI: https://doi.org/10.1021/je010075y
|
| [38] |
Kim S A, Yoo K P, Lim J S. High pressure isothermal vapor-liquid equilibria for the binary system of carbon dioxide (CO2)+1,1,1-trifluoroethane (R-143a). Korean Journal of Chemical Engineering, 2010, 27: 1887–1891. DOI: 10.1007/s11814-010-0293-5
|
| [39] |
Madani H, Valtz A, Coquelet C, et al. (Vapor + liquid) equilibrium data for (carbon dioxide + 1,1-difluoroethane) system at temperatures from (258 to 343) K and pressures up to about 8 MPa. The Journal of Chemical Thermodynamics, 2008, 40: 1490–1494. DOI: 10.1016/j.jct.2008.06.002
|
| [40] |
Sanchez C J N, Czubinski F F, Barbosa J R Jr, et al. Experimental data and Cubic-Equation-Of-State calculations of CO2/R-161 Vapor-Liquid equilibrium. The Journal of Chemical Thermodynamics, 2022, 165: 106635. DOI: 10.1016/j.jct.2021.106635
|
| [41] |
Valtz A, Coquelet C, Baba-Ahmed A, et al. Vapor-liquid equilibrium data for the CO2 + 1,1,1,2,3,3,3,-heptafluoropropane (R227ea) system at temperatures from 276.01 to 367.30 K and pressures up to 7.4 MPa. Fluid Phase Equilibria, 2003, 207: 53–67. DOI: 10.1016/S0378-3812(02)00326-6
|
| Sample | Diameter/Thickness (µm) | Length (µm) | {\alpha _\text{eff} } (mm2⋅s−1)@ \sim 290 K |
| PAN wires[60] | \sim 0.32 - 4.62 | \sim 23 - 126 | \begin{array}{*{20}{c}} {0.135 - 0.177} \end{array} |
| CNCs[57] | 0.334 | 142 | 1.58 |
| SiC microwires[56] | 34.29 | 1495 | 2.89 |
| CNT bundles[61] | \begin{array}{*{20}{c}} {222 - 280} \end{array} | \begin{array}{*{20}{c}} {2370 - 2770} \end{array} | \begin{array}{*{20}{c}} {13.2 - 29.6} \end{array} |
| CVD graphene on PMMA[59] | 0.45–1.74 nm thick graphene on 630–826 nm thick PMMA | \begin{array}{*{20}{c}} { \sim 2000} \end{array} | \begin{array}{*{20}{c}} {0.5 - 1.3} \end{array} |